Brianna Davis, Victoria Land, Lauren Marbury, Angela Tan, and Kidan Williams

The ten days of Girls Talk Math camp at UMD was arguably the best ten days of our summer. We spent these ten days learning about RSA cryptography and all the math that we needed in order to understand RSA cryptography. All of the teachers were kind and helped us through our packets of work.

During the camp, we learned about RSA cryptography. But, in order to do so we had to have some more math skills. During the first week, we learned about modular arithmetic. Modular arithmetic is used to find remainders of two numbers when they are added or multiplied together and then divided by another number, n. For example, [5] + [7]= [0] when n=12 because 5+7=12, and 12 is evenly divisible by 12 so there is no remainders. [6]+[11]=[5] when n=12 because 6+11=17 and when 17 is divided by 12, there is a remainder of 5. Also, we learned about Z. For example, [9] times [3]=[1] in Z13 because 9 times 3 equals 27 and 27 divided by 13 has a remainder of 1. This is the use of modular arithmetic.

We also learned about prime factorization and greatest common divisors. To factor a number down to just primes, you need to find primes that multiply together to get the number. For example, if you want to factorize 8, it is 2 times 2 times 2. For greatest common divisors, you find the prime factorization of both numbers, and find all the numbers that match up and multiply them together. The final number you get is the greatest common divisor. Next, we learned about what relatively prime means. For two numbers to be relatively prime, the numbers have to have only one factor, 1. For example the numbers 3 and 8 are relatively prime to each other because they only share one factor which is 1.

Finally, we learned about the Chinese Remainder Theorem. The theorem stated that the phi of one number, x, is equal to the phi of two other numbers, y and z, is y times z equals x and if y and z are relatively prime to each other.

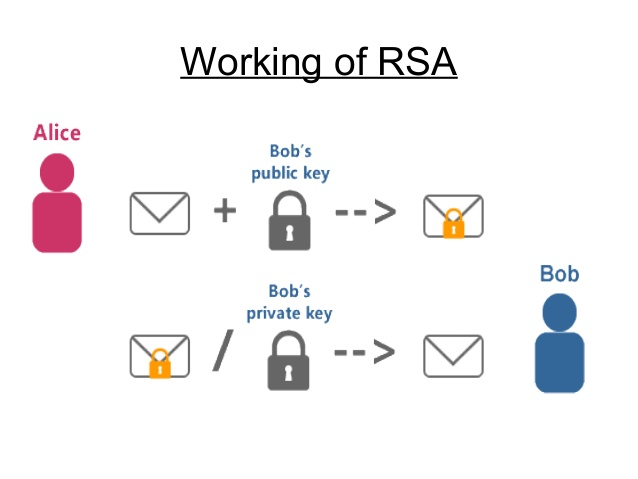
Now that we had finished learning about all of the math that needed to be learned, we started to actually learn about RSA cryptography. So to start, you would need to choose two primes. For example, 5 and 7. Then, you would multiply them together to get the value of N which is 35. Then, you find the phi of 35 which is 24. From there, you use the equation st = p times phi of 24 + 1. P being any number that makes the numbers s and t relatively prime to N (35) and that s times t equals 1 mod (phi of N). From there we get that p is 9, and then we get that 9 times 24 plus one is 217. Then, the only two numbers that satisfy s and t is 7 and 31. We make (s, N) our public key that everyone knows, and (t, N) our private key that no one knows but yourself. The alphabet corresponds to a number, ex. A=1 B=2 etc. If you wanted to send the letter B to Bob, you would raise the number 2 to the s power and then take that number and mod (N). Keep in mind that you are using Bob's public code values for s and N. If you wanted to decrypt a message that was sent to you, you would take the number that they send to you, for example 28. You would then raise 28 to the 31 aka t power and then take that number mod(35) aka N. The number you get would then correspond to one letter in the alphabet.

RSA needs quite the amount of math and hard work but the end result is definitely worth it. In fact, many existing encryption systems in the world today use techniques similar to the ones used to build RSA. That includes every time you use a password to sign in to your favorite website, or when you use your credit card to buy that special something online.

The main take away from this is that in this world, the battle is always between cryptographers and cryptanalysts. Cryptographers use complicated math to come up with new ciphers while the cryptanalysts are constantly trying to break them. Like yin and yang there is light where there is dark. So far, the cryptographers have had the upper hand with RSA, because these encryptions have remained secure but that may not stay true in the near future. For instance, with the existence of a full purpose quantum computer, RSA may not be as secure as it is today. So the scientists of the world are already looking for new and secure ways to keep your personal information safe and in a post quantum world. At the end of the day, remember to be careful as to how and where you decide to put your personal information because in the Information Age, information is power.