Dinah Aguilar, Meklit Amare, Jordan Dorsey, Nandi Edwards, and Lauren Witter

Our group Meklit, Jordan, Nandi, Dinah and Lauren studied Knot Theory at UMD. Knot Theory is the mathematical study of knots that has applications in many distinct areas of mathematics including algebra and geometry, as well as areas outside mathematics, like physics. So far we have studied female mathematicians like Erica Flapan, we have also experimented with the Knot Theory with hands on activities.

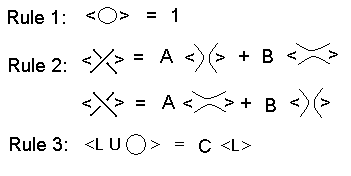
It first we learned an overview about Knot Theory like the basics of knots and links, the Bracket Polynomial, the Jones Polynomial. A knot is simply a loop in 3D space that doesn't intersect itself. The most basic knot is a circle. There are different kinds of polynomials because they help find different invariances and different parts of the equations.

The Bracket Polynomial works by modifying each crossing in the diagram, so we are eventually left with a collection of unlinked unknots. The goal is to define the knots with a polynomial.

Using brackets work by modifying each crossing in the diagram, so that we are eventually left with a collection of unlinked unknots. The way we used to experiment with knot theory is by using string and pipe cleaners to demonstrate the crossings.

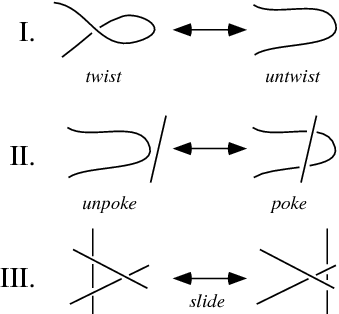
Untwisting knots uses the three Reidemeister moves. A polynomial invariant is when two knots equal the same polynomial. This is an important tool for identifying whether the knots are different knots or equal knots. The simplest knot is a circle and all unknots equal this knot.

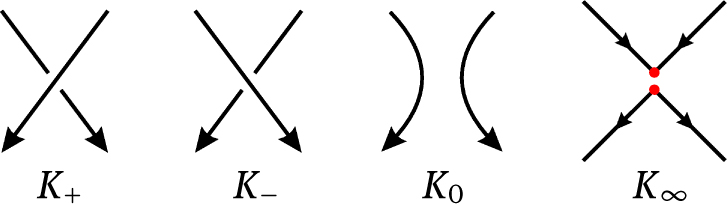
An oriented knot is an oriented link of one component, or identical, it is a knot which has been given an orientation. So for example if a line crossing is going down then that means the writhe number for that not well be negative, then if a line crossing is going up then that means the writhe number well be positive.