Girls Talk Math Camp — Promoting girls in math

NETWORK SCIENCE: A JOURNEY INTO MODERN DATA SCIENCE

Authors:

Jennifer Greer and Liliana Gordon

ABSTRACT:

Network science is the study of how groups of entities are connected through a series links, called edges. By studying the various properties and components of a network and the phenomenon it is based off of, deeper insight can be gained that enriches and highetns a scientists understanding. There are many applications such as image segmentation, cancer research, and social media, that use network science to gain a deeper understanding. Yet, because it is a new field there is still much to learn. Network science as a discipline is expanding every day because of the growing importance in data collection and analysis.

INTRODUCTION:

Over the past two weeks here at camp our group has been studying a new type of data modelling and analysis called Network Science. We are connected to the outer world through a series of complex relationships and links. Network Science is the study of these relationships.

BASICS:

The most basic components of a network consist of nodes and edges. Nodes are the entities are variables in the network. The edges are the links that connect those nodes. The nodes and edges of a network affect the structure, properties, and functionality of any given network.

Furthermore, a network is a group of nodes that are connected through edges. A network graphically represent data obtained from any given situation and utilizes it for further calibration and analysis. This is what Network Science is all about. Network science deals with how we use the networks to understand a situation better. However, you only use a network when the role of the nodes and links depends on the system's connections.

For instance, a few goals of studying network science are in understanding a system's robustness. Another possible reason in correlating a system's structure to its function.

PROPERTIES:

There are many properties of a network. Most of which we have not and cannot cover in this blog post. A few of them include centrality, directness vs. indirectness, weights, and degrees.

CENTRALITY:

Centrality is a property that deals with the relative importance of each node in a network. There are two types of centrality. One is called degree centrality. It is calculated when degree of node d is divided by maximum possible degree (when graph is simple) m, the number of edges in the network. Generally, this method is simple and intuitive. A more complex property of centrality is betweenness centrality. This is a type of centrality in which you take into account how the shortest paths between different nodes in network pass through node intersect.

DIRECTED VS. UNDIRECTED:

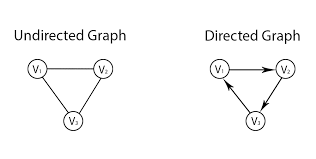
A graphical representation network can be directed or undirected. This basically means that the nodes within a network can be directed into a specific direction or may not be.

Consider Figure 1 below. On the right-most graph, there are are a series of arrows that point to a specific node. This is a directed graph. The left-most graph is an undirected graph. It is just a series of straight lines.

WEIGHTS:

Weights are numerical values assigned to edges on a network. Their significance within a network, mostly depends on the context. In a friendship network (a network that deals with interpersonal relationships), weights can measure the strength of any two people's relationship.

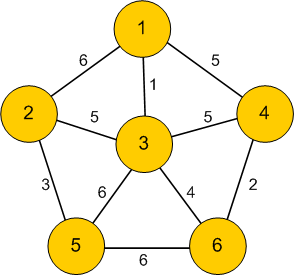
Consider Figure 2 on the left. In this network, there are a series of numerical values (1-6) that are assigned to specific edges. While these weights can have any significance, it is reasonable to assume that in this situation, the weight signify the distance from any two nodes.

DEGREES:

Degrees are arguably the most easy property to understand. A degree is the measure of how many edges are connected to a node. For instance, in Figure 2, the node 1, has a degree of 3, because it is directly connected to nodes 2, 3, and 4.

TYPES OF GRAPHS:

Some of the types of graphs are real, random, euler circuits and paths, hamiltonian circuits and paths, BA Circuits, and ER Graphs.

REAL:

Real graphs are networks that are based off of actual phenomenon and events. Furthermore, the connections that represent actual relationships within the situation. They typically have more clustered (simply put connected) nodes. Additionally, the probability of each node to have a similar connection is irregular and inconsistent.

RANDOM:

Random graphs are networks that are connected together without an actual reason or just randomly put together. These are literally the opposite of real networks.

EULER PATHS AND CIRCUITS:

Euler Paths are paths that can have 2 odd degree vertices or no odd vertices and every edge is traversed once while Euler Circuits can have no odd degree vertices, the circuit starts and ends at the same point and every node is traversed once.

HAMILTONIAN PATHS AND CIRCUITS:

Hamilton Paths do not have to start and end at the same point and traverses every vertice while Hamilton Circuits have to start and end at the same point and traverses every other node once.

HISTORY:

Let's talk a little bit about the history of network science. There is not much history about network science but because Graph Theory is closely related to network science so we can look at the history of Graph Theory to give us some of an idea of the history of network science. Our group chose what we thought were the top four important figures that contributed to Graph Theory and Network Science which are Leonhard Euler, William R. Hamilton, Wolfgang Haken, and Albert-Laszlo Barabasi. Leonhard Euler is credited for creating the first theorem of Graph Theory, wrote the first major paper for graph theory, and created the Seven Bridges Problem. William Rowan Hamilton created the Icosian Game that requires a specific path in order to win the game and the path was later called Hamiltonian Circuit. Wolfgang Haken solved the four colors problem that was presented over a year ago by Thomas Guthrie. The four colors problem is can you color a picture using only four colors and have the same colors not next to each other or adjacent to one another. When Wolfgang Haken solved the problem this led to the discovery of another application in Graph Theory. Albert-Laszlo Barabasi discovered that many real world networks followed a common pattern.

WHAT IS GRAPHY THEORY?

After reading all of this, what is Graph Theory? Graph theory is the representation of data set and relational data. This is also an area of pure mathematical interest like algebra and calculus. You would use Graph Theory to model something such as chemical compounds.

APPLICATIONS OF GRAPH THEORY:

Some of the applications of graph theory are in computer science, chemistry, operations research, and graph coloring. The applications of Graph Theory in computer science include data mining, image segmentation and programming languages. The applications of Graph Theory in chemistry are listing chemical isomers and modeling chemical compounds. The applications of Graph Theory in operations research are mostly found in transportation networks to model the transportation commodity between places. The applications of Graph Theory in graph coloring are similar to the four colors problem except you are using graph theory to understand the nodes and edges and whether the picture can be colored using minimum amount of colors. Python is one of the programming languages that are huge in Graph Theory and Network Science because you can use Python to find the shortest routes in operations research, finding the connections in chemical compounds, and in coloring the graph using a minimum amount of colors.

CONCLUSION:

Notably, there is so much more to network science then what we have presented to you in this blog post. Multiple algorithms and theorems are being developed everyday that better implement and analyze networks. And, while it is very easy to get caught up in the details of the methodology, network science is becoming more important in our modern day world. Our world is expanding. So we need to find new, more practical ways to store this data. This solution can be found in network science.

-------

If you are studying network science, don't freak out. It took us a long time to sort through the packet and do research. Here are some sites that we found very helpful: