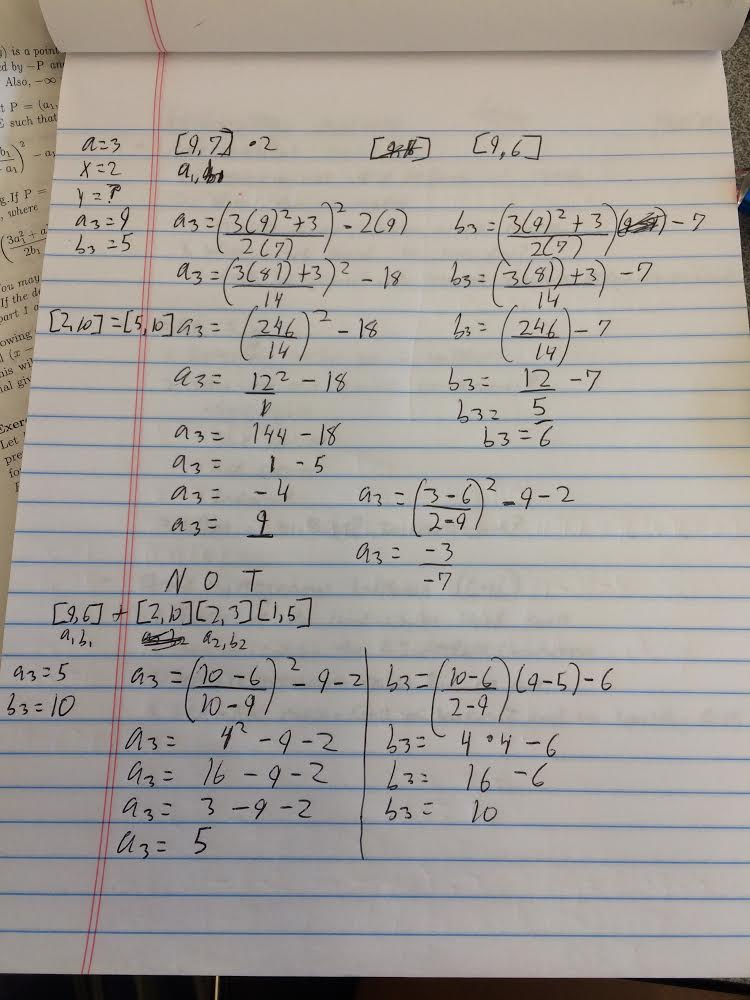Courtney Kim, Nevaeh Montgomery, Sofia Popol, Iris Xue, and Naomi Wilson

How do you communicate with a friend in complete secrecy while standing in a room full of people? "Elliptic-curve cryptography (ECC) is an approach to public-key cryptography based on the algebraic structure of elliptic curves over finite fields." ECC is simple, but secure. It utilizes concepts such as modular arithmetic, modular notation, finiteness, arithmetic, Zp when P is prime, group theory, isomorphic groups, generators, finite fields, and the list goes on. Over the course of 2 weeks our group has worked diligently to master these concepts, and learned the basics of ECC. Although we are touched on the surface of ECC, it has already made a huge impression on how we view math and communication.

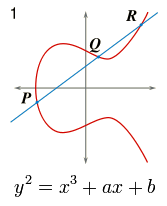
ECC is made up of many concepts, but the final goal is simply communication. Ideally, when using ECC, there are certain parts of the code known to the public and other parts that are only known by one person. Each person chooses a number within E(F) - for example; if the you're working in F_6 you could only choose 0,1,2,3,4, or 5 as your number, this is also known as "a" and "b". Both people must do a mathematical computation based on the variables they know. You can do this by using the point addition and point doubling formulas. These formulas will provide the points on the elliptic curve. If each person calculates correctly, the code should be revealed. Using ECC, we can create a secure, but simple way to send a message. If an observer who does not know the private key wants to figure out the message, they would have to do a lot of computations because of the complexity of "The discrete log problem". However, using the private key, the intended receiver would be able to easily figure out the message.

It's fair to say that our group had many challenges while navigating this packet. Our ages range from 14-17 (grades 9-12), and more than half of us haven't even started high school. The topics that we are now being introduced to aren't typically introduced until somewhere in the middle of college. Each one of us are completely different learners. Some could handle the packet rather quickly and independently while some of us needed more time and help to finish the packet. Because of this, we really took our time in understanding this ideology to the fullest possible extent. We've been incredibly lucky in having two counselors always at our side to help. Because of them we have been able to complete our packets. Today as we finished up our preparation for the presentation tomorrow, we were able to describe our topics in depth. This has been a great project!