Patterns and Fractals

Esther Awe, Excellence Herbert, Olivia Miller, Amiyah Turner, and Adalia Winters
Iterative Functions
An iterative function is a function that repeats itself. An initial input x0 is run through the function to get the output x1. This output is then used as an input in the same function to get the second output x2. Essentially, the function runs multiple times using the previous output (x value) as its input.
f(x0) = x1
f(x1) = x2
f(x2) = x3
...
f(xn)=xn+1
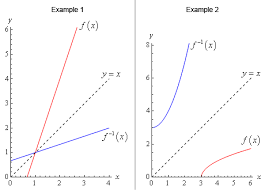
Inverse Functions
To iterate backwards or reverse a function we use inverse functions. While a function takes an x value and outputs a y value, inverse functions are used to get back to the original x value. A function is inverse by solving for x instead of y as seen in the process below.
M(xn) = xn – 1
xn = M-1(xn) – 1
M-1(xn) = xn + 1
Inverse functions are also one-to-one, meaning there can only be one x value for every y value, and this can be determined using the horizontal line test.
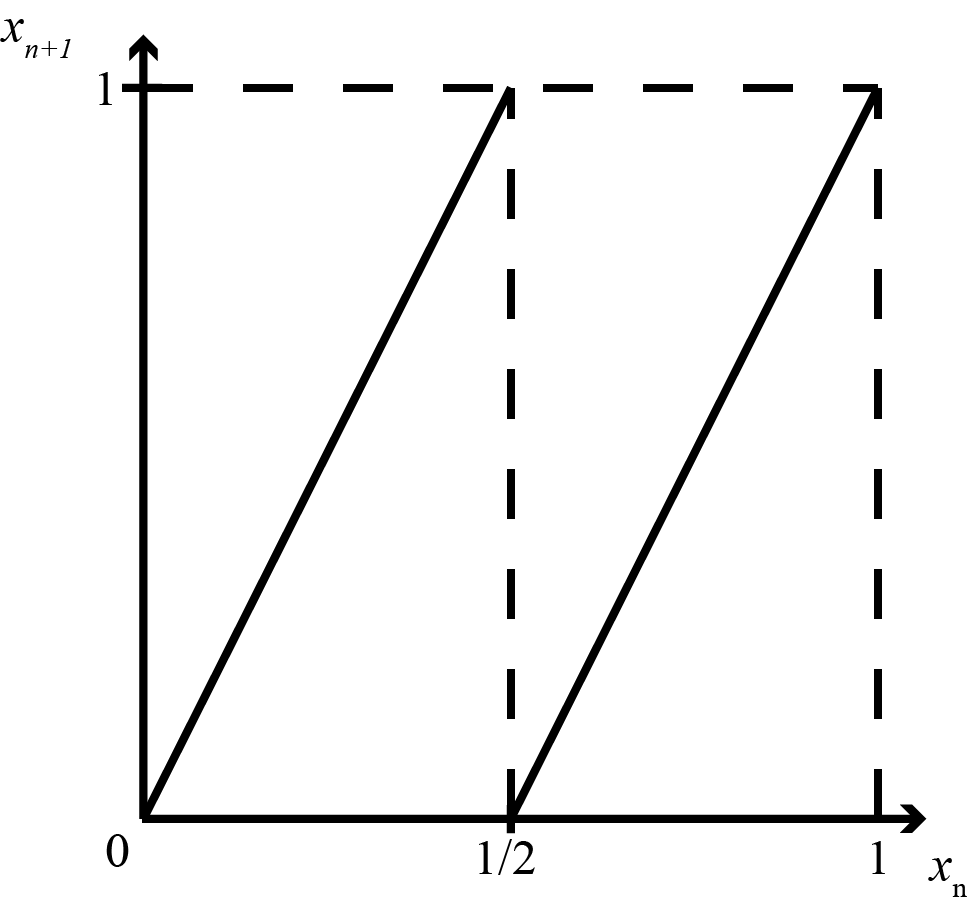
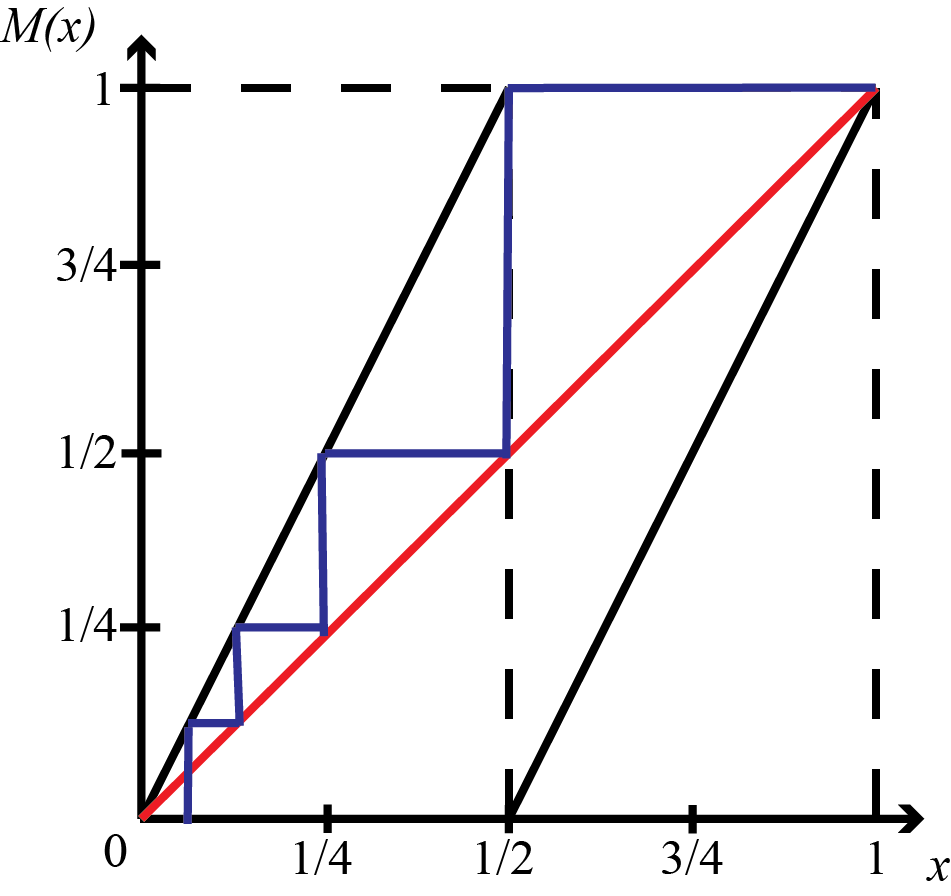
Mod Maps
Mod maps can be used to predict the pattern of behavior that a modulus function has. Modulus functions have no inverse since more than one x-value produce the same y-value.
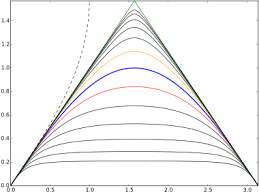
Fixed Points
A fixed point of a function is the point where the x value is the same as the y value. The value is found at the intersection of the graphed function and the line y = x or where xn = xn+2 in the graph on the left. In this function one can calculate the fixed points using 2p-2.
*Element: Any one of the distinct objects that make up the set
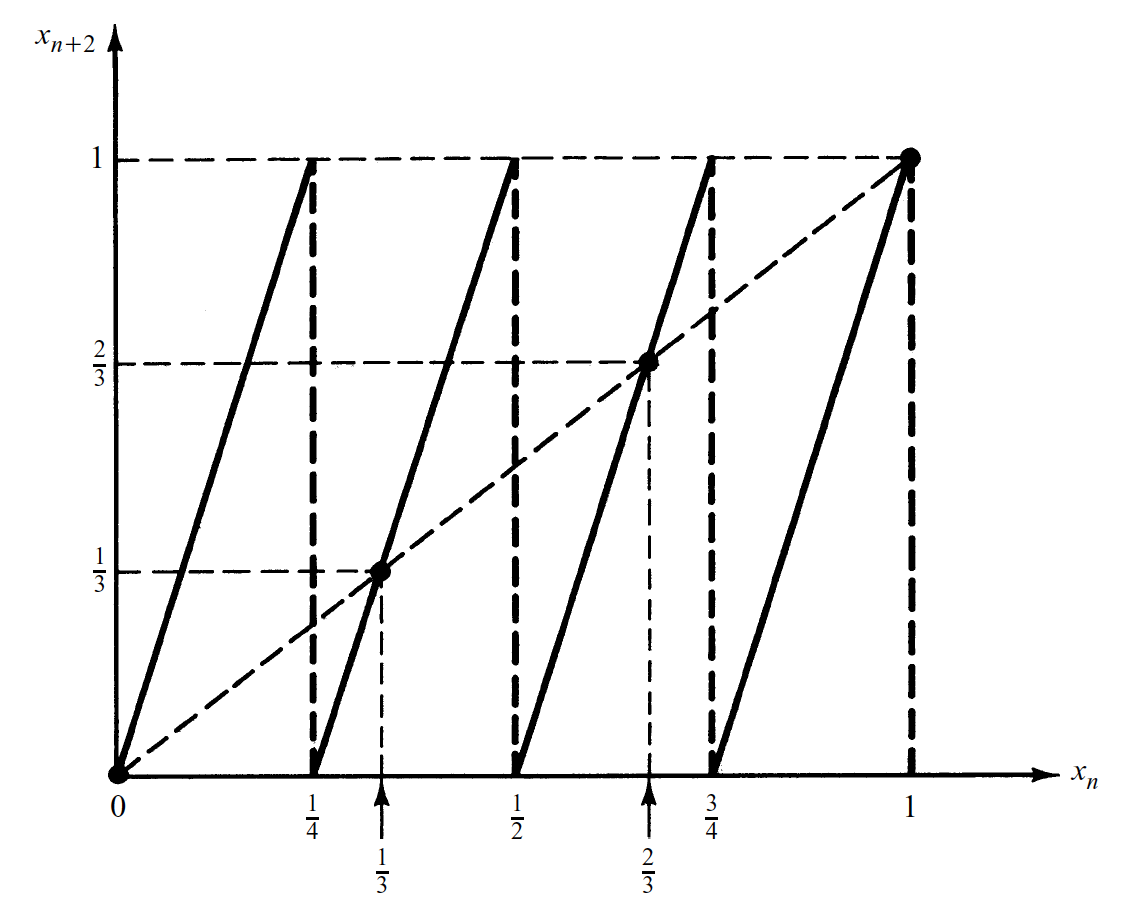
Convergence, Divergence and Cobweb Maps
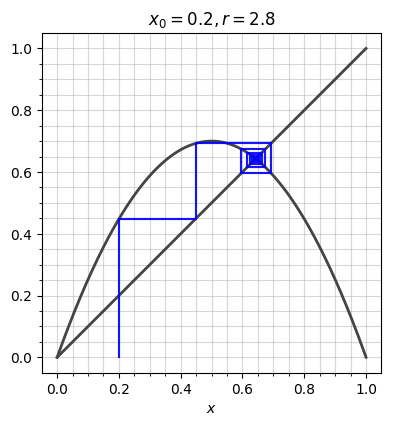
Diverge: When a function approaches positive or negative infinity (±∞). In this cobweb map M(x) diverges for certain initial conditions where M(x) approaches positive or negative infinity.
Converge: When a function approaches a fixed point/number. In this cobweb map M(x) converges for certain initial condition if M(x) approaches a constant valued fixed point.
It is easy and helpful to visualize divergence and convergence in Cobweb maps. When the cobweb inverts on itself, the function converges. When the cobweb spins outwards, the function diverges. On the left is a more incatrite cobweb map.
Fractals
A fractal is a never-ending pattern. Fractals are infinitely complex patterns that are self-similar across different scales. One part of the fractal is the same as the whole of the fractal. With the proper resolution, a fractal can be enhanced infinitely.

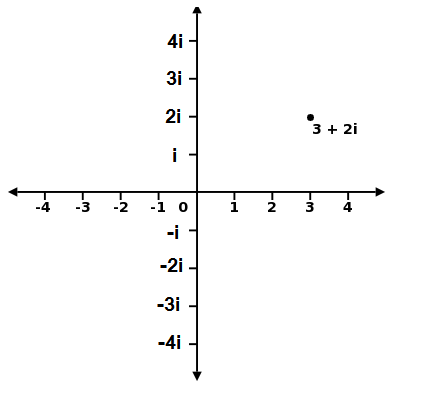
Complex Numbers
Previously we have been working with iterating a real-valued number, x. We will now be discussing the imaginary number which can be defined as i = √(-1). The square root of a negative number has no real valued solution but instead has an imaginary solution. We denote* a complex number to be the sum of the real and the imaginary numbers by z = ai + b. In this equation Im(z)=a is the imaginary part of z and Re(z)=b is the real part of z. In the figure on the left we can visualize complex numbers by representing the real part on the x-axis and the imaginary part on the y-axis. This shows we can visualize the complex-valued iterations of the Julia Sets and Mandelbrot Sets on a 2D plane.
*Denote: Stand as a name or symbol for
Julia Sets
A set of complex numbers that do not converge to any limit when a given mapping is repeatedly applied to them. Occasionally the result is a connected fractal set.
To graph Julia Sets the function f(z)=z2+c, where c is a constant, and both z and c are complex numbers represented by the form a + bi. The function f(z) is iteratied and the various colors represented in the graph are determined based on the number of iterations the function runs before it escapes the set bounds. The brighter the color, the more iterations it takes for the function to escape, with black being that the iterations do not escape the bounds. See cover photo for the Julia set when c = -0.1+0.65i.
Mandelbrot Sets
A particular set of complex numbers which has a highly convoluted fractal boundary when plotted. Using the same equation mentioned in the Julia sets, the “c” value varies and initial condition, z0=0. For a particular c, if the orbit stays bounded under iteration, c is in the Mandelbrot Set. If c diverges, it is not in the Mandelbrot Set.
