Nina-Netanya Enwesi, Carla Hernandez, Ivy Liang, Isabella Macdonald, and Shayla Reid

Introduction

Number systems are an essential part of the mathematical and computer science world. Number systems consist of many bases, each of which are a way for computers to represent numbers. In general, the act of computers receiving and storing data utilizes the number system. They define certain numbers and are important to the computer system as a whole. The most common number systems are binary, decimal, and hexadecimal.

Decimal (Base 10)

The decimal system was first invented in India, between the sixth and seventh centuries. It contains 10 single digits, namely 0-9. Most people are most familiar with this because it is the system we use daily, be it in a math class or a job setting. Each position of the digit represents a multiple of a power of 10, since 10 is the base of this particular system. For example, in the number 542, the 4 is the tens digits, and is represented by 4 x 10¹ in the decimal system.

Binary (Base 2)

The binary system is the most common system used by computers. It is a system that consists of two numbers: 0 and 1. Each piece of binary code is called a bit and is used to represent different characters while utilizing the binary number system. Each position and digit represents the multiple of a power of 2, the base of binary. Because the binary system only has two digits, it is the most simple system to master, which is why we started our number system journey by exploring binary numbers.

Hexadecimal (Base 16)

The hexadecimal system or as we know as the base 16 system contains 16 digits. The word “hexadecimal” means sixteen because of how “hex” means six and “dec” means ten. This system contains not only ten numbers (0 - 9) but also six letters (A - F) to replace the double-digit numbers. The digits and positions of this system represent different powers of 16. This means that the rightmost digits represent a multiple of 16⁰.

Other Common Number Systems

Other common number systems include Base 20 and base 36. In base 20 the digits 0-9, as well as the letters A-J, are used to represent the numbers. Each number place in this system represents a power of 20, but we are limited by the number of letters in the alphabet. With that brings us to Base 36. In base 36, the digits 0-9 as well as ALL the letters in the English alphabet (A-Z), are used to represent the double-digit numbers. If we wanted to go to higher bases we would have to begin to add other symbols to represent single digits.

Importance of Number Systems

As mentioned before, number systems play a huge role in the world of computer science, especially the binary system, since it is the most used system for computers to store information. Computers use bits and bytes to represent different data types in order to present information to the everyday person. One byte is equal to 8 bits. This is another way to compact bits together.

Hexadecimal digits are also important. One hexadecimal digit is 4 bits and there are 2 hexadecimal digits in 1 byte. There are some cases when using hexadecimal digits are more efficient than binary digits. For example, hexadecimals define locations of memory data points. In addition, they can be used to define color in the form #RRGGBB: red, green, and blue. Sometimes, hexadecimals are able to represent and group binary code in a more user-friendly manner.

In our packet, we learned specifically about Internet Protocol version 4, or IPv4. We were taught how to convert those IPv4 addresses from a long chain of binary data to decimal form, a form that we were all more familiar with. Each IPv4 address has 32 bits or 8 bytes.

Computer Data Storage and Data Transfer

In many commonly used computer languages such as C/C++ and JavaScript, the programmer is required to tell the computer the type of number you are using beforehand. This is because the computer needs to be able to understand how to store it, perform various calculations, and understand how to read it. This is a very important step. Computers also have a finite amount of storage and are not able to contain all the numbers in the world. A computer can use either 32 or 64 bits to store an integer.

Floating Point Representation

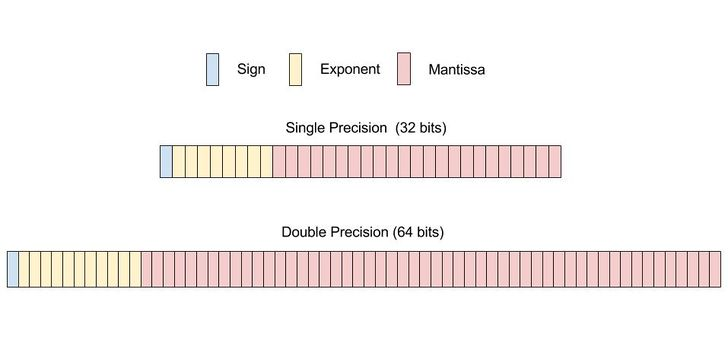
Up to this point, we have never attempted to represent decimals and fractions in different bases. Yes, it is a bit more complicated, but still possible to do by using something called floating point representation. A float is a name for the version of a floating point number, also called single precision. In a float, there are three different groupings of bits: the first bit tells the sign of the number, the following 8 bits are called the characteristics, and the last 23 bits are called the mantissa or the significand. In 32 bits, the general formula of conversion is: (-1)^sign x 2^{exponent - 127} x (1 + mantissa).

In addition, we can go through a similar process with 64-bit floating point numbers, also called double precision. Similar to single precision, the first bit of the chain will determine the sign: 0 for positive and 1 for negative. However, the next 11 bits represent the exponent/characteristic, while the last 52 bits are the mantissa/significand. The formula for both single and double precision are very similar as well. For double precision, the general formula of conversion is: (-1)^sign x 2^{exponent - 1023} x (1 + mantissa).