Evelyn Young, Ayanni Lanier, Natalia Wilson, Jen Chan, Lailie Rosius, Iris Xue

What is graph theory and network science?

Graph theory is the study of mathematical structures called networks. (examples: spread of disease, social media, communication and population increase/decrease). Network science is a field that applies the mathematical results of graph theory to study network models of real world problems using things like Python and computer programming.

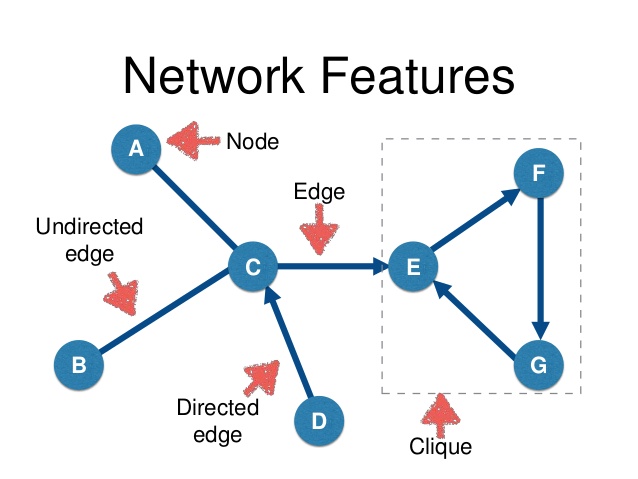
• Networks are structures made from nodes and edges. Nodes are drawn as points or circles, which represent objects.
• Edges are the lines between nodes which represent relationships between the nodes.

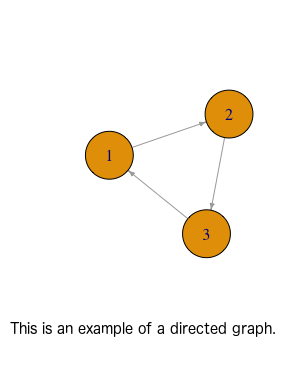
Directed vs Undirected

• Undirected networks are networks where the direction of relationships doesn’t matter (or they go both ways).
• Directed networks are networks where relationships aren’t reciprecol (they don’t go both ways). The directions are very specific.

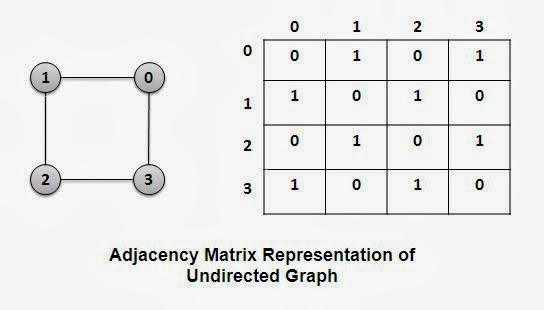
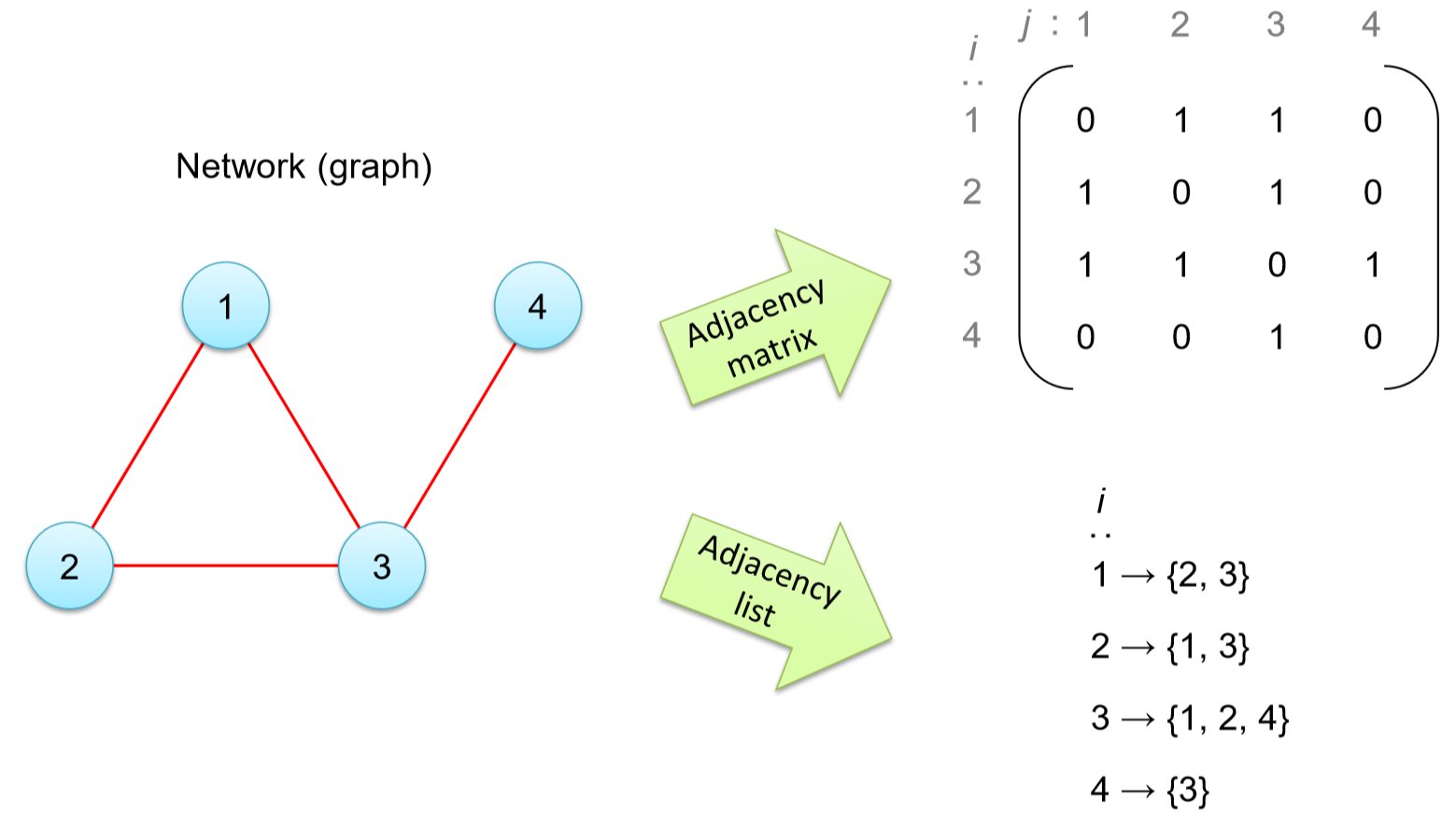
Adjacency Matrices

• A matrix is a mathematical object that can be thought of as a table of numbers. It has an index notation of [A]_i,j where i is the row number and j is the column number. If there is an edge from node i to node j the entry is 1, otherwise the entry is 0. Can be multiplied to find different nodes.
• Adjacency List is a list of each node followed by a list of only the nodes to which it has an edge. It is easier to see which node as an edge connecting it to another node since a matrix table is mostly filled with zeros. A matrix that is more than half filled with zeros is called a sparse matrix.

Paths vs Cycles

• Path: a sequence of adjacent notes starting with i and ending with j.
• Cycle: a path that starts and ends at the same node (vercity).

Eulerian Paths and Cycles

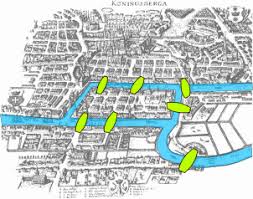
• The seven bridges of Königsberg is considered to be the first problem ever studied in graph theory. Swiss mathematician Leonhard Euler is the first person to solve the problem of investigating if it was possible to walk through the city, crossing each bridge once.
• An Euler path must include two or less odd degree vertices.
• A Euler path is a network that crosses every edge exactly once.
• A Eulerian cycle is an Eulerian path that starts and ends at the same node.
• A connected undirected network has an Eulerian path if and only if at most two nodes have odd degrees. A connected undirected network has an Eulerian cycle if and only if all nodes have even degrees.
• Two most common methods for finding Eulerian paths are Hierholzer’s algorithm and Fleury’s algorithm.

Hamiltonian Paths and Circuits

A Hamiltonian path is when each vertex is visited one time. A Hamiltonian circuit is when each vertex is visited one time and ends at the starting node.

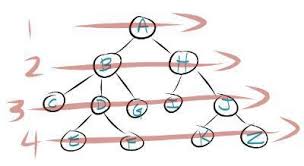
Breadth-First Search

• An algorithm used to find the shortest path in an unweighted network by starting at node s and ending at node d.
• This algorithm is accomplished by searching the network in “layers”.

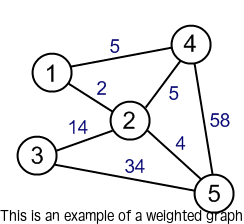
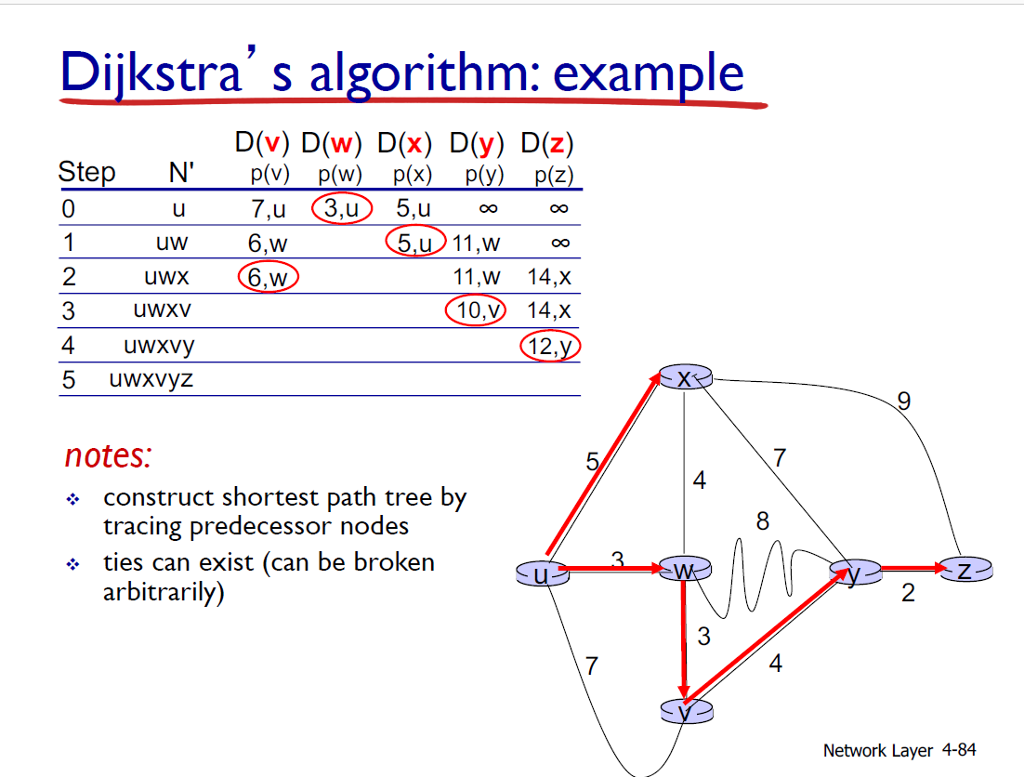
Dijkstra’s Algorithm

• An algorithm used to find the shortest path in a weighted network.
• This algorithm is accomplished by recording the shortest subpath and parent from each node.