Micah Chandler, Ava Lancaster, and Chioma Opaigbeogu

What is number theory?

Number theory is the study of whole numbers and their properties. It is considered to be part of “pure mathematics,” and is still the subject of much active research done by mathematicians today. Number theory creates numerous famous unsolved problems and uses proofs to verify mathematical theorems.

Primes

Primes are numbers that can only be divided by themselves and one. There are an infinite number of primes. Primes are the building blocks of all numbers as shown through factoring every number greater than 1. When you factor these numbers, you can “break it down” into primes. Ex: 12=2²·3. 2 and 3 are primes that make up 12.

Modular Arithmetic

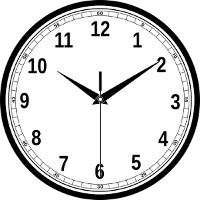
Modular arithmetic is when your answer must belong in a certain range of numbers. Like on a clock, the numbers must stay between 1 and 12; you loop back around to 1 once the hand has passed 12. Modular arithmetic is very similar to this. If you were trying to find 7 + 14 mod 4, you would add 7 + 14, which equals 21, but since that number exceeds our range of 4, you would then divide by 4. So, 21/4 = 5 remainder 1, and 1 is your answer.

Congruency

Let, a, b, and n be integers. We say that a is congruent to b if n divides a - b, or: a ≅ b (mod n) if n | a - b. What it really means for two numbers to be congruent mod n is that the result is the same after performing the modulus n operation.

Fermat’s Little Theorem

If p is a prime number and a is any integer not divisible by p, then ap-1 ≅ 1 (mod p). In accordance with the above rule regarding congruence we know that p will divide a^p-1-1,as long as the requirements stated above are kept.

What We Learned

The above topics are just a fraction of the things we learned in the two weeks that we spent studying number theory. We learned to do proofs and divisibility rules, as well as how to use the Euclidean Algorithm and Bézout’s Identity. We learned to persevere through problems that we didn’t understand at first and to keep working at it until we understood. Often times, just rephrasing the problem in a different way made us realize that we knew what we were doing all along! Though some proofs and problems challenged us in ways that we may not have expected, our team leaders made it possible for us to be able to tackle them through their ability to explain complex problems in a simple and understandable way.

Number theory may have little real world applications, but it is the backbone of many other math fields such as cryptography. Famous number theorists today include Jennifer Balakrishnan, Steven Galbraith, and a whole host of others. You may be more familiar with the old greats like Euclid, Father of Geometry, and Diophantus, Father of Algebra, and not to mention Pythagoras who is famous for his work with right triangles but who was also a famous number theorist. The possibilities of number theory is seemingly endless seeing as there are so many number theory problems still left to solve. We hope that after reading this you’ll feel encouraged to take a step into this field.