Mathematical Modeling (and its applications to epidemiology)
What is a Knot?
Epidemiology is the study of infectious diseases and prediction of its effects on a population.
Where and when was epidemiology originated?
Epidemiology originated in Circa 400 B.C, which means it is nearly 2,500 years old. Hippocrates attempted to explain disease occurrence from a more rational waypoint.
What is a mathematical model?
Mathematical models are things that take data and try to make sense of it to sometimes predict what will happen with that data in the future. There are many different type of models used in math modeling as different situations call for different models.
What are the different types of models?
Linear Models
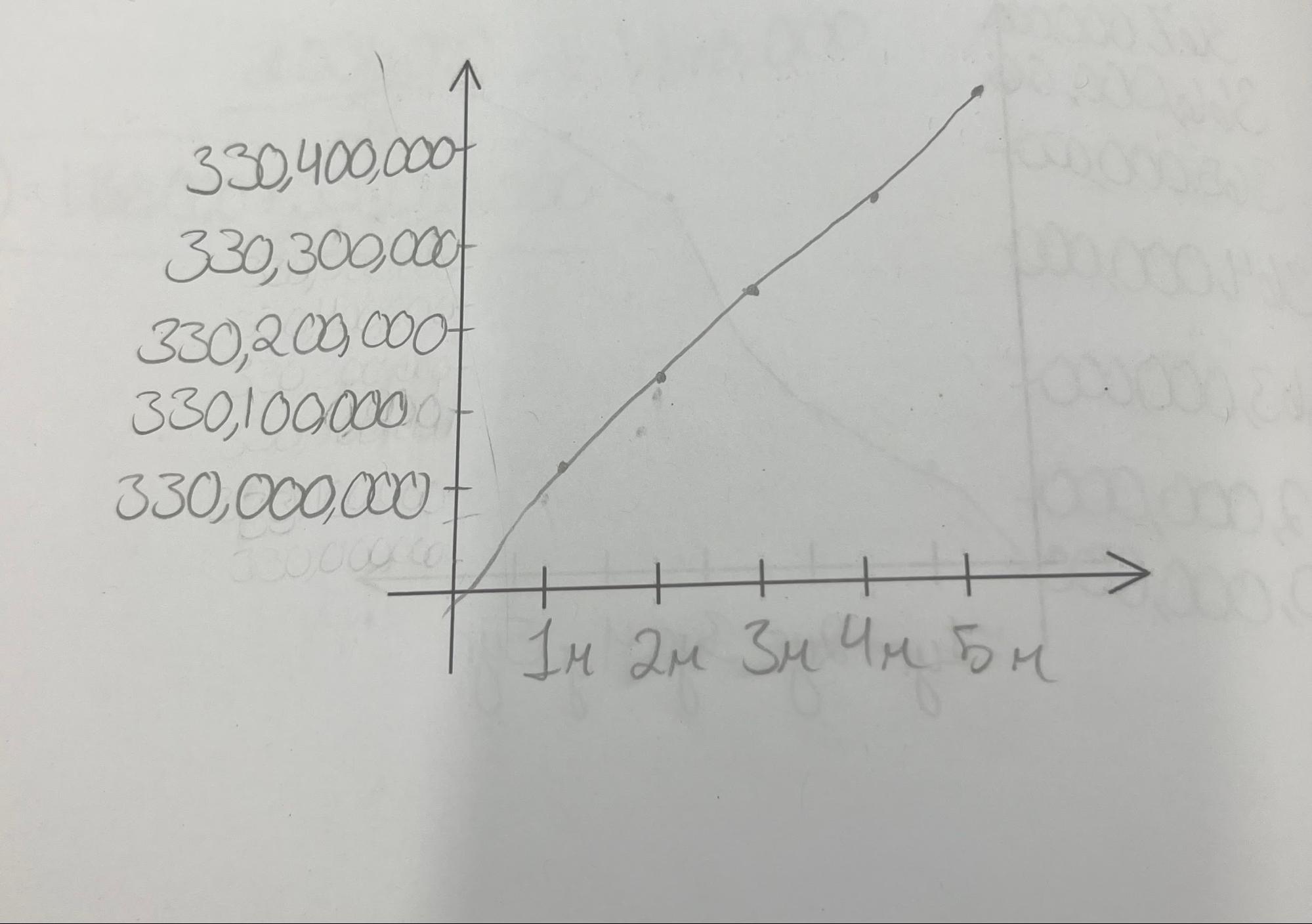
As you can see in the graph, the line is straight or, “linear,” hence the name. The function, P(t)=mt+b is what we used for some of the graphs which you may have noticed uses the slope formula, y=mx+b. T is the number of years or any given unit of time measurement and P represents population. The other function we used for linear models was P(t)=a t+P(0). In this case P(0) is the initial population and a is a constant called a parameter. Parameters are the parts of the model that incorporate real information and can very depending on what they are measuring.
Nonlinear Models
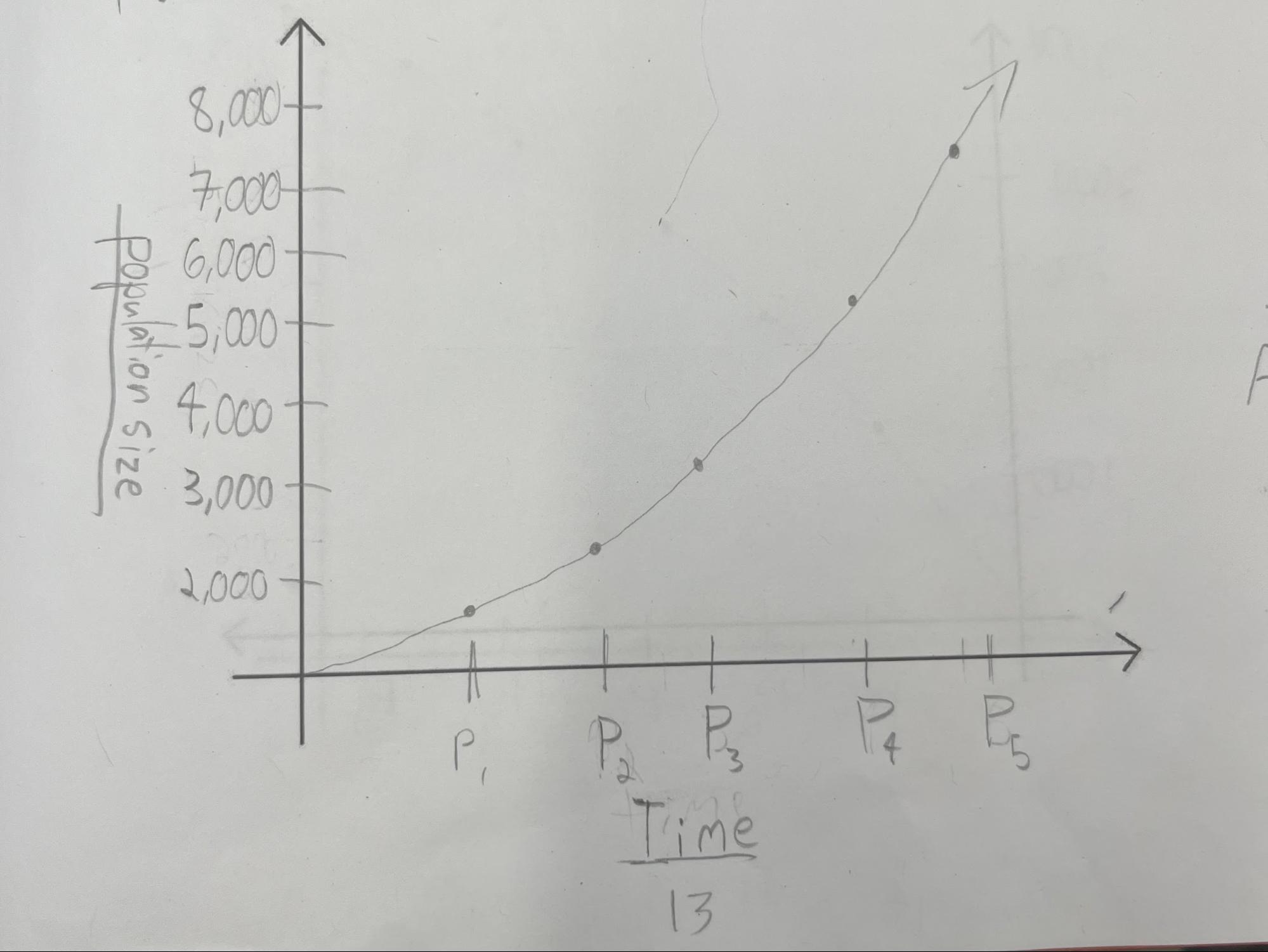
A nonlinear model describes nonlinear relationships in experimental data.
Discrete Models
Discrete models are used to predict the population in distinct or, “discrete,” amounts of time.
Exponential/Geometric Models
A mathematical model in which the variable is in the exponent and the graph increases or decreases slowly at first, then more quickly. An example of this is population growth
Logistic Models
A logistic Model is a common non-linear population model. The formula for P(t+1)=R P (1- pt/c) where is rate constant and C is parameter related to something called the carrying capacity
Why are models in math so important?
Mathematical models give us the freedom to be able to understand the spread of a disease over a population and how the disease affects the population. Without these models it would be a lot harder for epidemiologists to get a clear visual of how a disease is affecting the population. Making the process to control the disease takes more work and time than it would if epidemiologists had a model for reference.
How do these models connect to epidemiology?
There are specific mathematical models used in epidemiology called SIR models. SIR stands for susceptible, infectious, and recovered (also sometimes know as ‘removed’). The susceptible group is the whole population who has not gotten sick yet and is vulnerable to getting the virus. The infected group is the people who are actively sick (also they are most likely contagious to the S group). The R group, as previously stated could be called ‘removed’ or ‘recovered’, the reason for this being if one dies, they would be in the R group and technically if one were to be dead some people may not consider that to be ‘recovered’, which is why it is sometimes called ‘removed’ instead. People who are immune to the disease are also in the ‘removed’ category. Anyways, in a SIR model the people in the R group cannot infect the S group. SIR models can be graphed and used to predict future rates of infections of a disease. If you have heard of when people said we had to ‘lessen the curve’, they were referencing these epidemiological models. It should be noted there are many factors that go into account in making these models. For example, vaccines. If people got vaccinated it may affect the susceptible group (by lowering their susceptibility) or the I group’s rate of infection to the S group. There are also models in epidemiology that account for other factors such as if infants are born immune to diseases (MSIR models). And many other models we will not be discussing but feel free to do your own research!
Why does all of this matter?
Mathematical models used in epidemiology can help predict what methods or policies could be used for management of disease. For example, social distancing and masking were examples of methods used to lessen the spread of covid-19 when it was very active. Without epidemiologists, infectious diseases would be less predicted and may have greater devastating effects on a larger amount of the population.
Conclusion
Overall, epidemiology might seem like another boring type of mathematics but little did you know it means so much more than that. Now you know a little more about epidemiology and how people use it in jobs or real world crises. I hope this blog informs you a little more and we hope to hear from you and your feedback about our blog.