Graph Theory
What is Graph Theory?
Graph Theory is the exploration of numerical structures that describe connections between objects. Graphs are made up of dots (called vertices) and lines (called edges) that connect the dots. Each dot represents something, and the lines show how these things are related. By looking at the connections between the dots, we can understand how they are organized and how we can move from one dot to another. This helps us find paths or routes through the structure. Graph Theory has many real-life applications and helps us solve problems by understanding and analyzing these connections in a simple and organized way.
Types of Graphs
An Euler Path is a route through a connected graph such that each edge of the graph is used exactly once. An Euler Circuit is a special type of Euler path where the route starts and ends on the same point. The properties of these graphs are used to solve problems about optimizing circuits.
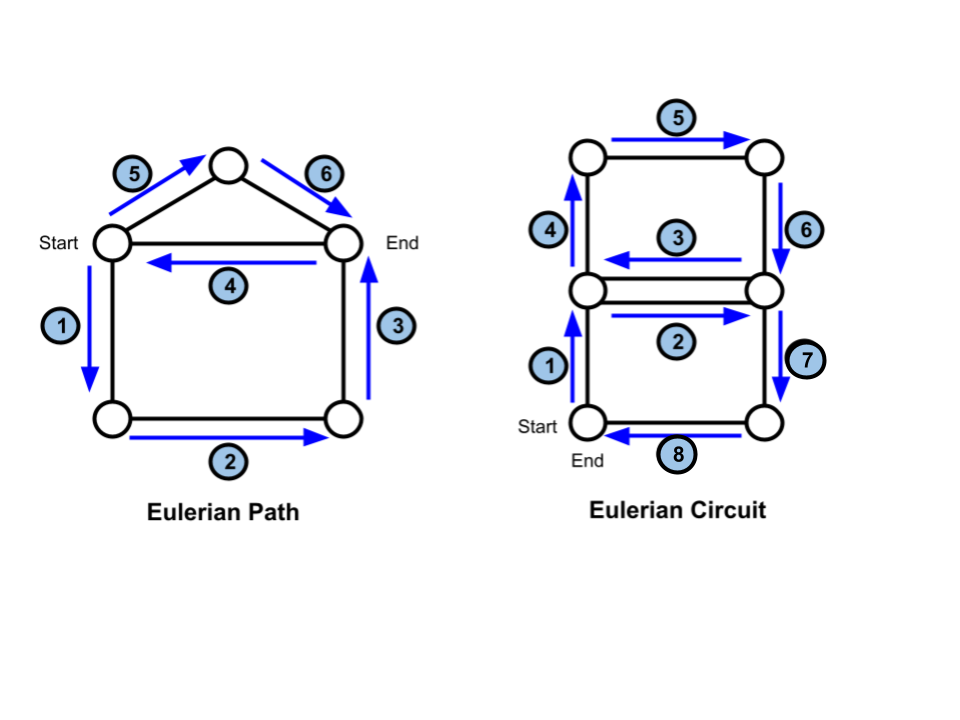
We can determine whether a graph has a Eulerian path or circuit by looking at the degree of the vertices. The degree of a vertex is the number of edges connected to it.
A graph will contain an Eulerian path if there are no more than two vertices with odd degree. Similarly, a graph will contain a Eulerian cycle if every vertex has an even degree.
Matrix Notation
We can depict graphs in matrix notation. A matrix is a rectangular array of numbers. An adjacency matrix is a matrix that is used to represent a graph. The numbers in the matrix represent the number of edges between two vertices.
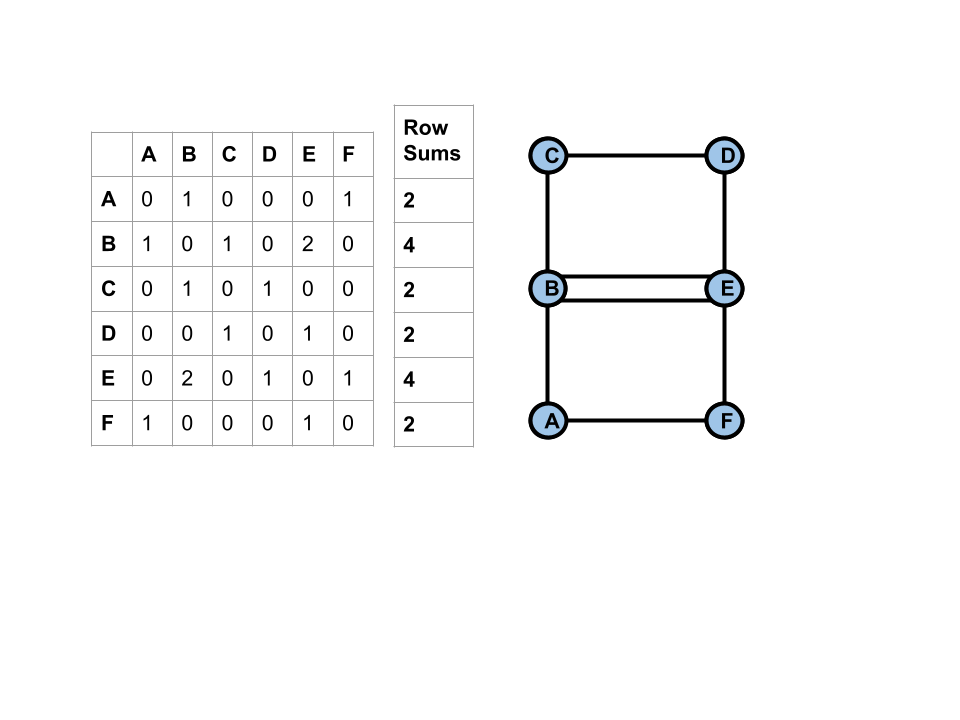
We can determine whether a graph has an Euler circuit by looking at its adjacency matrix. By summing all numbers in a row, we can find the degree of a vertex. If all of the row sums are even, we can say that the graph has an Euler circuit.
Graph Coloring
Vertex coloring is a technique that uses graphs to solve problems related to avoiding conflicts. In this method, we assign different colors to the vertices of a graph, ensuring that no two adjacent vertices have the same color. The goal is to minimize the amount of colors needed.
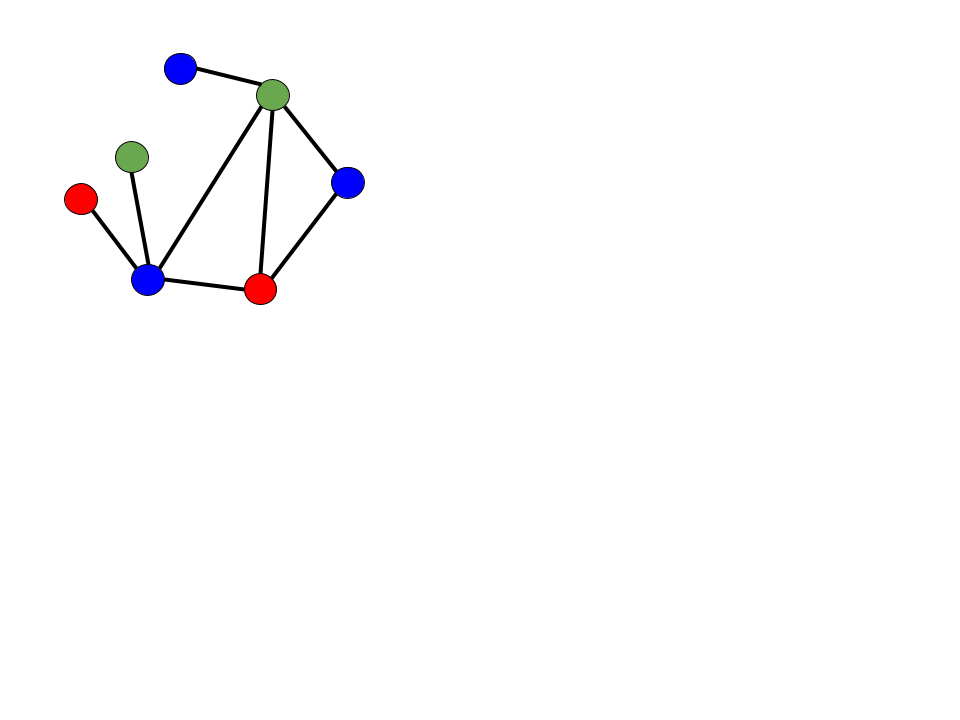
Graph coloring enables us to address issues related to resource allocation, scheduling, and task assignment.
An example of this is assigning radio frequencies. We can represent radio stations with vertices and signal interferences with edges. Using graph coloring techniques, we can ensure that no two adjacent stations share the same frequency while minimizing the number of different frequencies used to avoid signal interference.
Graph Theory in Real Life
Graph Theory is a field of mathematics that has many practical uses in real life. One famous example is the Seven Bridges of Königsberg problem.
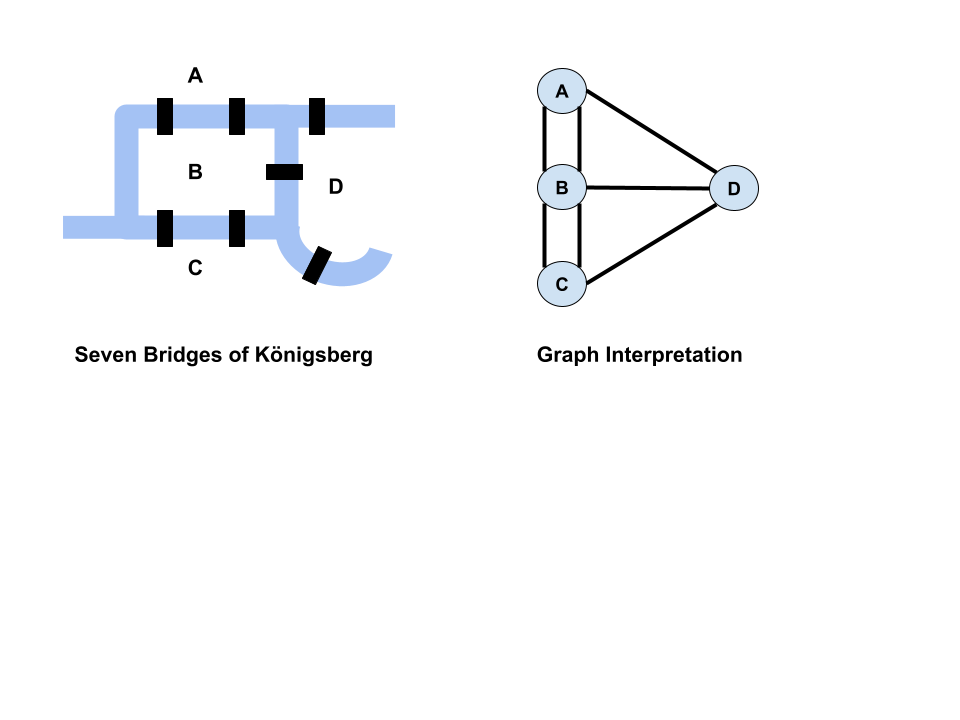
In 1736, mathematician Leonhard Euler showed that it was impossible to walk through a city and cross each of its seven bridges exactly once. This discovery highlighted the significance of graph theory in solving real-world problems.
Graph theory is applied in everyday life, like in Google Maps. By representing road networks as multi-graphs, Google Maps considers factors such as different routes, lanes, and road types. Algorithms analyze the network efficiently, considering real-time traffic and user preferences. This helps Google Maps provide accurate directions, guiding users along the most efficient path to their destination.

Social media networks, often classified as star graphs, represent connections between individuals. In this structure, a central node (celebrity or influencer) is connected to multiple peripheral nodes (followers). The central node has a high degree, while the peripheral nodes have lower degrees. This hierarchy gives the central individual higher visibility and reach.
Why is Graph Theory important?
Graph Theory helps us understand and solve problems involving connections and relationships. It provides a way to represent and analyze systems like social networks, transportation networks, and computer networks.
With graph theory, we can find efficient paths, identify patterns, and optimize resource allocation. It allows us to make better decisions and solve complex problems in a structured way.