Knot Theory
What is a Knot?
Shoelaces. Sewing. Waistbands. All of these everyday activities have one thing in common: knots. But did you know that there are over six billion types of knots documented? While knots may seem like something for convenience, they are really a fascinating mathematical concept that is a part of pure geometric mathematics.
Unknot

Left-Handed Trefoil

Right-Handed Trefoil
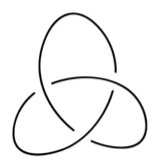
Figure-eight knot
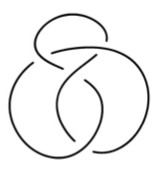
Square knot
The mathematical definition of a knot is a closed 3D curve or loop that doesn’t intersect itself. A knot cannot be untied to result in a circle. The most simple type of knot is a circle, which is called the trivial knot, or more commonly, the unknot. Some types of knots are pictured below:
Hopf Link

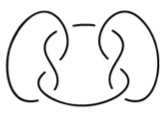
Solomon Link
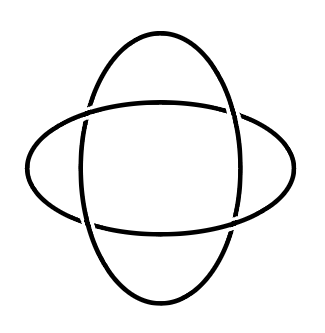
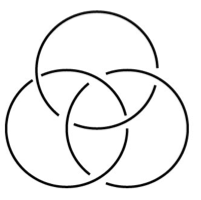
Borromean Rings
Reidemeister Moves
One of the main issues that mathematicians deal with is differentiating knots from each other, and determining whether knot diagrams represent the same knot or not. This is where the Reidemeister Moves come in. Named after mathematician Kurt Reidemeister, these moves are used to manipulate knots to compare their diagrams. There are three moves:
R1: Twist move - twist or untwist a crossing (intersection) in either direction.
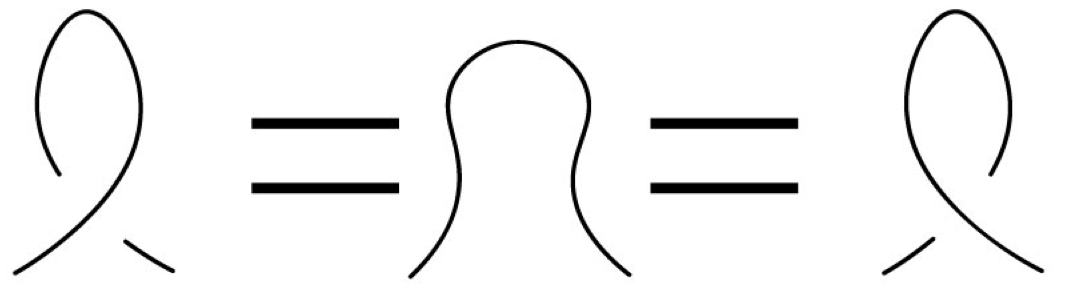
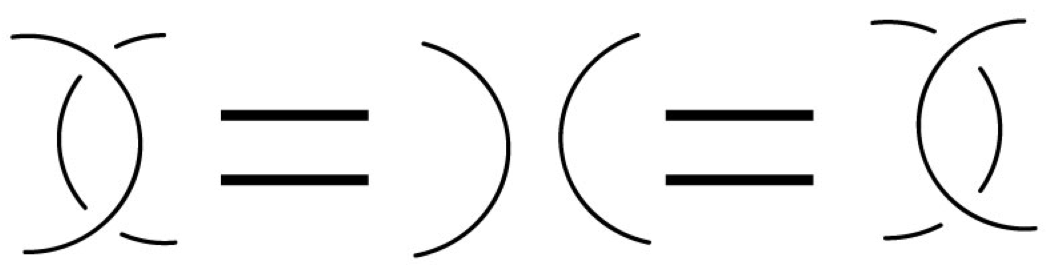
R2: Poke move - move one loop over another.
R3: Slide move - slide a string over or under a crossing.
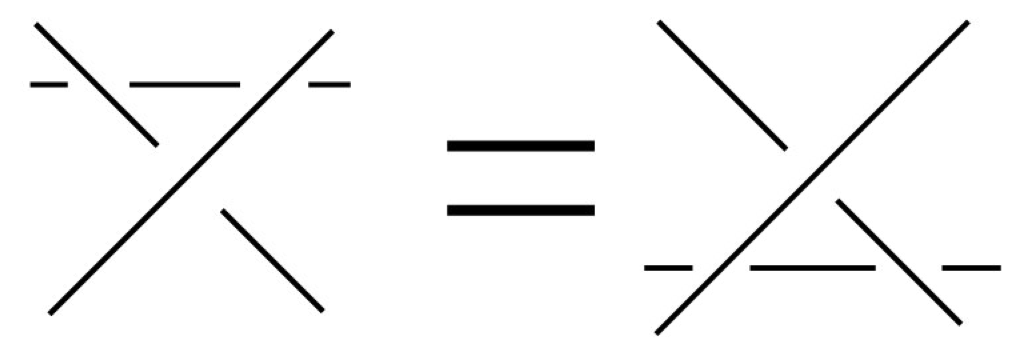
While these moves may change the knot diagram, they do not change the knot itself. Because of this, they can be used to show that two knot diagrams represent the same knot. If two different knot diagrams are related by a sequence of the three moves, they represent the same knot.
The Jones Polynomial
Mathematicians have developed different methods of distinguishing knots from each other. One of the most effective methods is the Jones Polynomial.
First, let’s define different parts of the formula for the Jones Polynomial.
Orientation
Orientation is the direction that a knot’s strings are going. They are depicted by an arrow along the line of the knot diagram. Knots can go either clockwise or counterclockwise. The orientation of a knot determines the value of a crossing.
Knots have crossings; without crossings, it would be the unknot. However, every crossing is either positive or negative. One way to determine this is by using the right-hand-rule. By pointing your right hand in the direction of the top string and curling your hand in the direction of the bottom string, you determine whether or not the crossing is negative or positive by where your thumb is pointing. If it is pointing up or towards you, the crossing is positive. If it is pointing down or away from you, it is negative.
Writhe Numbers
The writhe number of a crossing depends on if it is positive or negative. The writhe number, defined as w(x), is equal to 1 if the crossing is positive, and -1 if the crossing is negative. We can also compute the writhe of a knot by adding up all the respective writhe numbers of the crossings of the knot. For instance, the left-handed trefoil has three crossings, all of which are negative. Therefore, the writhe number of each one is -1. Adding them all together, the writhe number of the left-handed trefoil is -3.
Now that you know these essential components for the Jones polynomial, we can apply it. The formula is this: q^(-2) J(D) - q^2 J(D)=(q-q^(-1))J(D), using a Skein relation. In order to compute this, you must compute the knot (D) using bracket polynomials, and find the writhe number w. If two knots have the same Jones polynomial, they are the same knot. While this may seem overwhelming, that’s okay! This is a really complicated math topic, and we were so lucky to learn about all of this!
Applications of Knot Theory
While knot theory may seem like a purely mathematical concept, it can be applied to other topics as well, most notably in DNA replication and transcription. During cellular division, DNA must replicate itself. DNA also transcribes proteins that are important for cellular activities such as cell growth. Knot theory comes in because in order for replication and transcription to effectively take place, enzymes must untangle the DNA. If we view DNA as a knot, we can use knot theory to make estimates about how hard different strands of DNA will be to disentangle. Using quantitative measures such as the writhe number, the ideal crossing number, and the unknotting number, scientists can estimate DNA unpacking more accurately and precisely.