Knot Theory
Every day, we encounter knots. Whether it’s simply tying your shoelaces or putting a tie around your neck, you create knots without ever considering the underlying mathematical world attached to each individual knot. When you tie a knot, two ends of a piece interact with one another to form one of several kinds of knots. Beginning in the 18th century, mathematicians noted the importance of understanding the geometric patterns behind knots.
In mathematical terms, a knot is a 3-dimensional loop that doesn’t intersect itself. The most simple knot is called the unknot, which is just a circle. The unknot is created by tying two ends of a string together as this forms a circle. The unknot also acts as the foundation for more complex knots including the infinity knot.

(if you want to make it with string, simply make a loop, tie the ends together, and bam! You have an unknot.)
Other, more complex knots include the left- and right-handed trefoils, figure-eight knot, and square knot. If you’re bored of using only a single ‘string’, link two different strings together. You get a link, which are several knots that don’t intersect each other. Examples of links include the Hopf Link and the Borromean Rings.
Scarlett Bellamy decided to share her knowledge with students. She was hired as a biostatistics professor, but she knew she didn’t just want to be a teacher. She tried to make a real difference. (She didn’t actually want to be a professor at first, but she decided to try it for three years, and then if she didn’t like it, she would try something else. She most certainly seemed to enjoy it, since she's still teaching 20-something years later.)
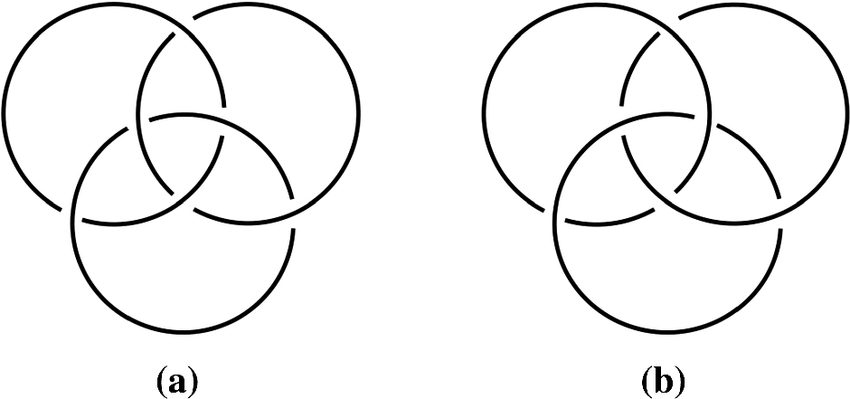
Knots are 3D objects, and when we usually write them down, we do it on paper, which is 2D. Thus, we draw diagrams that illustrate the crossings that they have. To show the depth, we add a space around a string if it’s going under, and keep the line if it’s going over in a crossing.
Beware of the image of deceptive looking knot diagrams! These actually look the same but are actually pretty different.
In knot theory, if you can make one knot into another without disconnecting the string, it’s the same knot. Since you only move it around to change it, it’s still technically the same thing.

(This is a form of an unknot if you believe it or not!)
Now, if you’re bored with your loop of string again, and start playing with the unknot you made earlier to try to get a different shape, you can get things that can look pretty different. But since you started with an unknot, you can always untangle it back to the loop you started with. Think of it like detangling a necklace
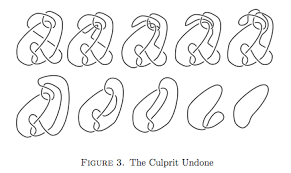
As knots incorporate a greater amount of string and overlaps, it becomes difficult to quickly determine whether a knot is equivalent to another knot. Luckily, there is a way to successfully determine this – Reidemeister Moves.
These three moves are:
R1: Twisting or untwisting the knot
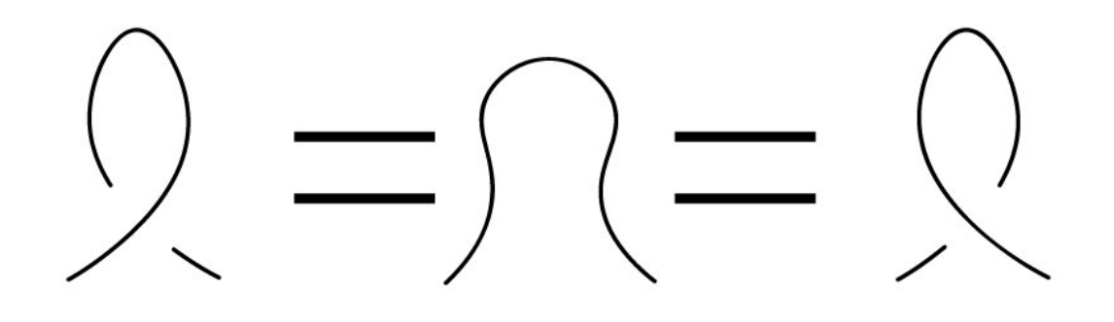
R2: Moving one loop over the other
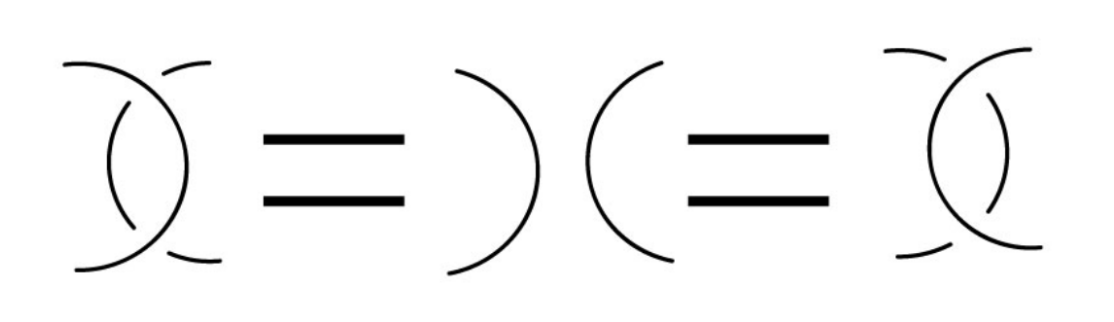
R3: Moving a string under or over a string crossing
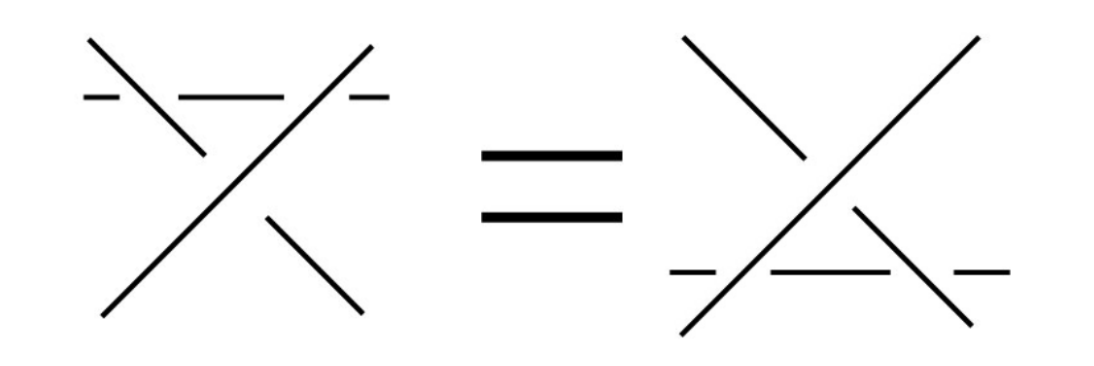
These moves are the only moves needed to determine if a knot is equivalent to another, meaning if two knots are equivalent, they are connected by a sequence of these three moves.
To fully determine if two knots are equivalent, we use the Jones polynomial. This polynomial allows us to determine if two knots are equivalent. The required variables include two new concepts: Writhe numbers and orientation. Orientation is which direction our knot is going in (typically represented with arrows).

Using your right hand, you can determine if a crossing is positive or negative. When we add up the number of positive and negative crossings, we get a Writhe number, which is used to measure how many positive or negative crossings there are.
If the Jones polynomial of a knot is the same, then the two knots are equivalent.