Group Theory
Instruction
During the past two weeks in the Girls Talk Math camp, we studied the topic of group theory. Group theory is the mathematical study of symmetry, or more specifically the study of a set of elements present in a group in abstract algebra. Group theory was invented in the early 19th century by Evariste Galois, some applications in the modern world being crystallography, solving a Rubik’s cube, quantum chemistry, algebraic coding, cryptography, and more.
Let's start with some fundamentals in euclidean geometry:
Different kinds of rigid transformations:
Rotation, translation, and flipping.

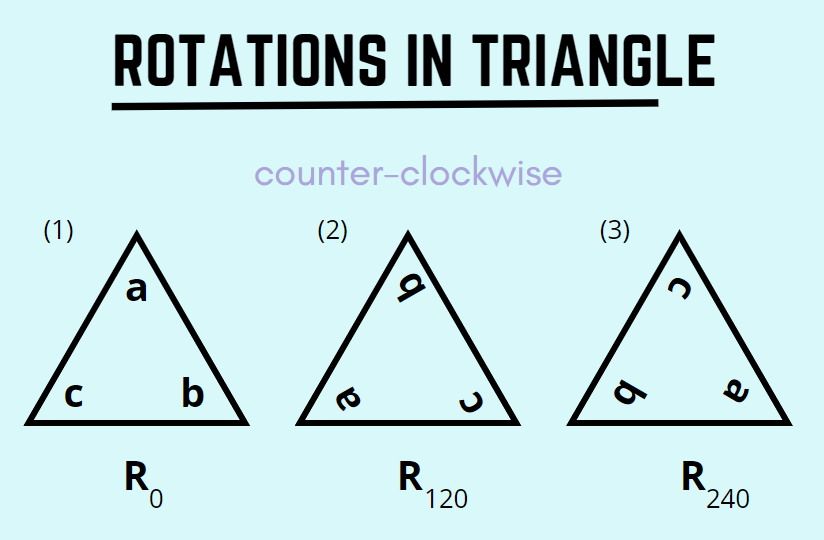
An equilateral triangle has 6 symmetries:
3 rotations: by 0, 120, and 240 degrees
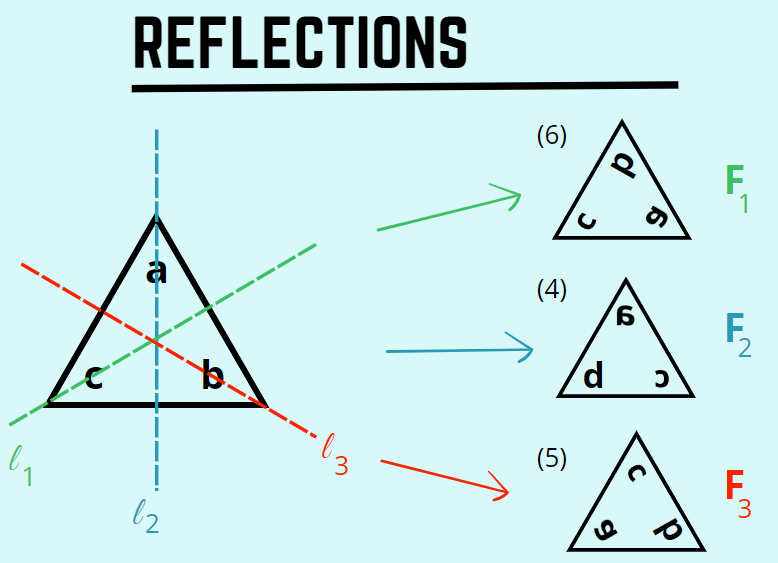
3 reflections: Flipping triangle across lines labeled L1, L2 and L3
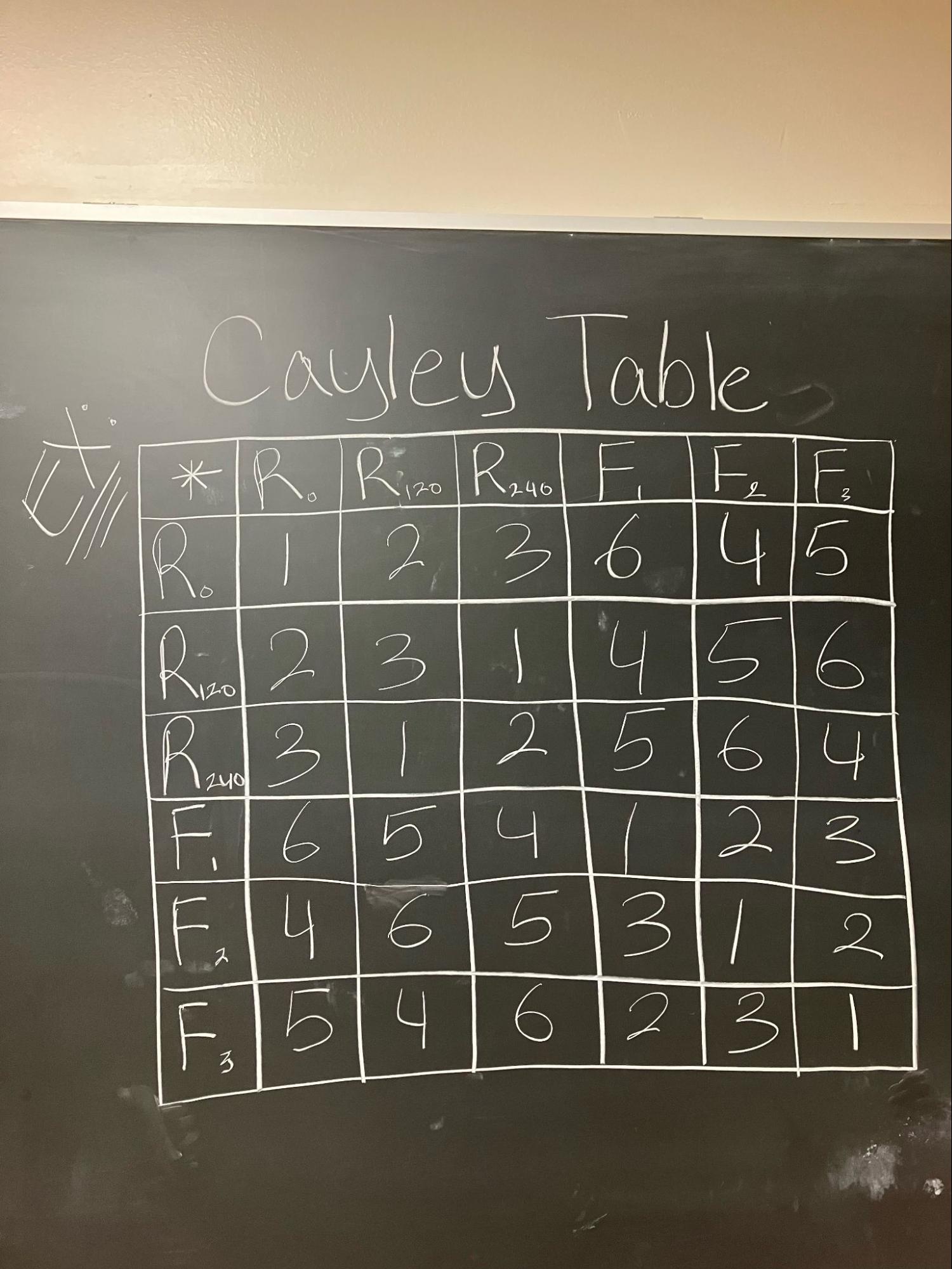
Definition of a Group
A set of numbers/shapes that have operations, associativity, an identity, and an inverse for each element e.g. D3 (the group containing every symmetry of a triangle as shown earlier).
Axioms of a Group
- Operation: All groups need to be able to achieve closure. If a and b are two elements of G (the group), then the third element c (the outcome of some function a * b) will also be a part of G.
- Associativity: All groups need to maintain the ability to be solved for the same result despite moving the location of the parentheses around: a * (b * c) = (a * b) * c.
- Identity: All groups need to have an element of G that is typically denoted by e, that multiplied by any element of G, will produce that element back: a * e = a.
- Inverses: All groups have corresponding elements for each element of G that "inverses" it, denoted as a-1: a * a-1 = a-1 * a = e.
Abelian or Not?
It is not always true that a*b=b*a. It is true for some pair of elements, in which case we say that a and b are commutative. If it happens for all pairs of elements of G, then we say that G is abelian (or commutative).
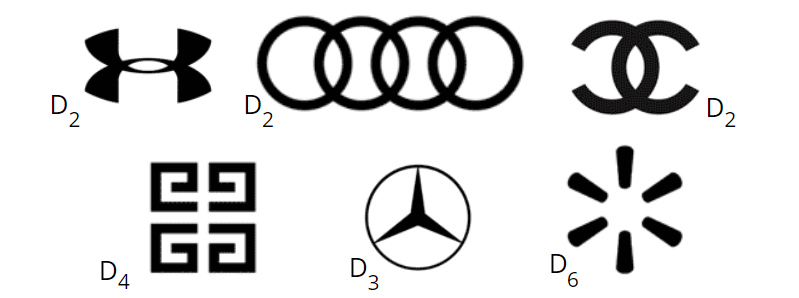
Dihedral groups (D) arise frequently in nature and in art. The logos and decorative designs on the picture below are some examples of dihedral groups of order 2, 3, 4, 5 or 6 (D2, D3, D4, D5 and D6).