Graph Theory
What is Graph Theory?
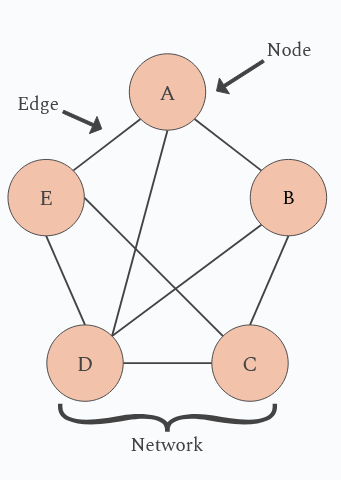
Graph theory is the study of graphs, also called networks, which is a type of mathematical structure. Networks display the relationship between the two main components of the graph: the nodes and the edges. The nodes, sometimes called vertices, represent the objects within the graph. The edges, sometimes called links, represent the relationships within the graph.
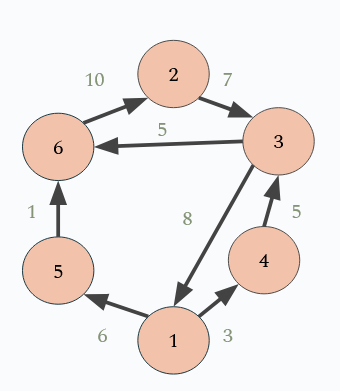
Directed and Undirected Networks
In graph theory, there are quite a few attributes that can be applied to networks, one of which being directed and undirected graphs. In undirected networks, the direction in which the edge is moving does not matter. When a network is undirected, there are either no arrows on the edges, or arrows on both sides of the edge; both show that the relationship between the edge and the adjacent nodes goes two ways. When a network is directed, that means that the direction in which each edge is going matters. One indication that a graph is directed is if the graph has arrows pointing in the direction the relationship is moving. Directed networks are additionally assigned in-degrees and out-degrees, which tells us how many edges are into a node and how many edges go out of a node respectively.
Weighted and Unweighted Networks
Another attribute that differentiates networks from each other is whether the network is weighted or unweighted. Weighted networks have a numerical value assigned to each edge, and unweighted networks do not. Weighted networks typically are representative of variables such as distance, time, or price when used in real world applications.
Paths and Cycles
An essential component of graph theory is locating paths and cycles in networks. A path is a chain of adjacent nodes that starts at one node and ends at another. Cycles resemble paths, except they start and end at the same node. Paths and cycles are generally assigned lengths–a path from node 1 to node 6 on the graph above would have a path of length 3. Similarly, if we wanted to make a cycle using node 6, a possible path would be 6 → 2 → 3 → 1 → 5 → 6, which is length 5.
The Use of Graph Theory in our Everyday Lives
Graphs have an unlimited number of real-world applications. Any concept involving an object and how it has a relationship to other objects could be represented by a network. For example, they are often used in transportation. A map of an underground train network is an example of this. The nodes would represent the different stations that the train would stop at, and the edges would represent the railways connecting the stations. Much like how mathematicians try to find different ways to get to different nodes in a graph, people will also use these maps to see how they can get to their destination or node through the different paths provided by the tracks or edges. Social groups, online networks, the nervous system–the subjects that could be portrayed by graphs are endless.
The Importance of Graph Theory
We are surrounded by graphs, and we use them every day without even thinking about it. Networks are an essential part of our everyday lives; without them, we would not have roads, nor would we be able to understand systems like the food chain, neurological networks, or the internet.