Surfaces
Throughout the 2 weeks of this camp we focused on the topic, surfaces. To have a proper understanding of surfaces, dimensions play a key role. Dimensions of an object are the numbers of directions it can travel. In other words dimensions are the number of choices the object can make for the directions. You might have heard of 1 dimension, 2 dimension, 3 dimensions, and even 4 dimensions. 1D can be expressed as something as simple of a line, 2D could be expressed as a flat shape, 3D consists of a length, width, and height like a cube, and an example of a 4D shape is a tesseract. Although most shapes can be well defined, some can not be well defined. For example when there is a point where it intersects in more than one direction that can be expressed as not well defined.
Now that we have what dimensions are, we can finally introduce the definition of surfaces. Surfaces are an object which looks 2-dimensional to a creature living on it. Many (polyhedral) surfaces have vertices, edges, and faces.
For those surfaces without vertices, edges, and faces like a traditional polyhedron, you might have heard of common examples of surfaces like a sphere, cylinder, and torus. In case you have not heard of these terms, a sphere is a figure so shaped that every point on its surface is an equal distance from its center. Cylinder is a solid geometric figure with straight parallel sides and a circular or oval cross section. Torus is a surface or solid formed by rotating a cylinder so that the top and bottom are connected. Now you may be thinking how do you actually make a surface. Making actual models of a surface can be easier for you to picture. With the help of squares and arrows we can examine surfaces in a simpler way. One major key component of understanding surfaces is the mobius band. A mobius band is a surface that can be created if you take a strip of paper, give it a half twist and then you would put the ends together forming a loop. A mobius band, also known as a mobius strip or loop, only has one surface, so if you were to draw a line starting from a point and continue until you finish the line, there will be a line on either side of the strip.
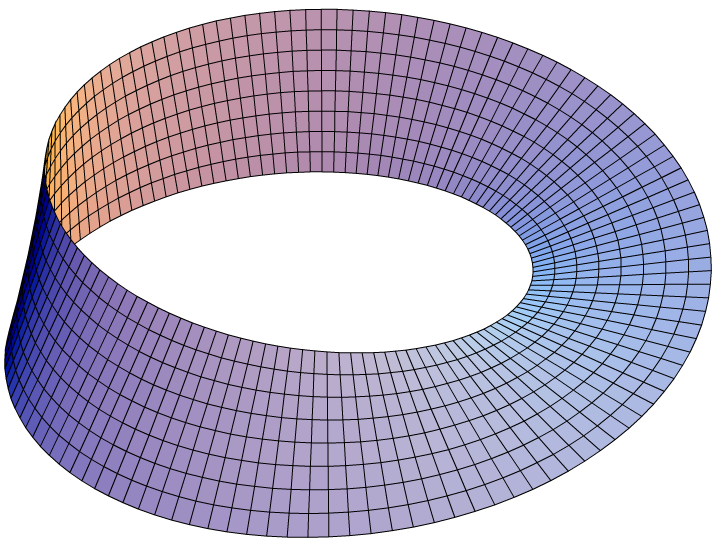
Another major component to surfaces are orientable surfaces and non orientable surfaces. Orientable surfaces have a consistent upwards direction everywhere on the surface. Non orientable is when it is not orientable so a mobius band can be non orientable because if you were to point upward and walk until you get back you wouldn’t be pointing in the same direction. However examples of orientable surfaces are a cylinder, torus, etc. This is the case because it has two sides in space. The number of vertices subtracted from the number of edges added to the number of faces is called the Euler Characteristic. The characteristic is an invariant of surfaces, meaning that it remains unchanged/constant. The formula is V - E + F. For any simple polyhedron (in three dimensions), the Euler characteristic is 2 besides a torus. Additionally homeomorphic shapes are two shapes that are homeomorphic if they can be bent or morphed into one another, without cutting, pinching, or collapsing into any part of the shape. Also remember talking about the Euler Characteristic, that also applies to homeomorphic shapes. Some examples of homeomorphic shapes are a sphere and a bowl, a cup and a torus.
Some additional information on the surface area interior point and an exterior point. We call a point in a surface an interior point if we can draw a small enough ball around the point that is completely contained in the surface, and doesn’t contain any points not in the surface. A point is an exterior point of a surface if you can surround it with a (appropriate dimensional) disk, where the disk lies completely outside the surface. Similarly, we call a point a boundary point of a surface if there is some small enough ball that contains some interior and exterior points (of the surface). The collection of all boundary points is called the boundary of the surface.
Finally, surfaces can be such an interesting topic if we get down to the basic information and advance from that. We have definitely learned so much from these two weeks of GirlsTalkMath and I am sure you have too from reading this. Thank you for reading!